4. Heapsort

4.1 Hintergrund

Heapsort ist ein algorithmisch interessantes, wenn auch kein schnelles zeitoptimales Sortierverfahren, welches entgegen Quicksort auch im worst case eine Laufzeitkomplexität von O(n*log(n)) besitzt. Ebenso handelt es sich nicht um einen Algorithmus nach dem "Teile-und-Herrsche"-Prinzip, jedoch wird auch hier durch eine Auswahl sortiert, wobei diese allerdings geschickt organisiert wird. Hierfür verwendet das Verfahren die Datenstruktur des Heaps (engl.: Halde), in welcher die Bestimmung des Maximums bzw. Minimums einer Menge von n Schlüsseln in nur einem Schritt möglich ist und welche sich dadurch für ein Sortierverfahren bestens eignet. Allerdings ist die Heap-Operation des Versickerns, welche dies ermöglicht, nicht trivial, sodass man über eine Komplexität von O(n*log(n)) nicht hinaus kommt.
Mit der Beschreibung des Heaps und der von uns benötigten elementaren Operation soll hier zunächst eine grundlegende Wissensbasis geschaffen werden, bevor auf das damit verbundene Heapsort eingegangen wird, welches dann nahezu trivial zu verstehen ist.

4.2 Die Datenstruktur Heap

4.2.1 Grundlagen:
Ein Heap ist im Grunde nur eine elementare Struktur zur Speicherung von Daten, wie es auch ein Stapel (Stack) oder eine Schlange (Queue) ist, nur dass die Daten hier in einer gewissen Art und Weise bereits vorsortiert sind. Deswegen spricht man bei Heaps auch von Prioritätswarteschlangen, was nicht über den Fakt hinwegtäuschen soll, dass es sich hierbei grundlegend nur um eine Folge von n vergleichbaren Schlüsseln handelt.
Die Ordnung, welche in einem gültigen Heap vorliegen muss, soll im kommenden Unterpunkt 4.2.2 verdeutlicht werden. Allgemein gefasst ist ein Heap ein Binärbaum, d.h. ein Knoten hat jeweils zwei Söhne (linker und rechter Sohn), was sich bei n zu speichernden Elementen E₀, E₁, E₂, ..., E_n-1 wie folgt darstellt:

Objektorientierte Realisierungen sind zwar denkbar, die interne Speicherung erfolgt allerdings meist über ein Array, in welchem das Element E₀ die Wurzel ist und allgemein die Söhne eines Elementes E_k E_2k+1 und E_2k+2 sind, da sich auf einer Ebene i des Binärbaumes maximal 2ⁱ Elemente befinden und somit effizient und eindeutig im Array gespeichert werden kann. Folgende Abbildung illustriert die interne Speicherstruktur eines Binärbaumes in Arrayform:

4.2.2 Heapordnungen:
Ein Heap kann in zwei möglichen Varianten implementiert werden. Bei der einen, dem sogenannten MinHeap liegt eine Min-Ordnung vor, beim MaxHeap auf der anderen Seite eine Max-Ordnung. Beide Varianten sollen nachfolgend kurz vorgestellt werden.

4.2.2.1 MaxHeap:
Ein Heap heißt MaxHeap bzw. es liegt eine Max-Ordnung vor, wenn für alle inneren Knoten deren Schlüssel größer gleich denen der beiden Söhne sind, d.h. es gilt die (Max-) Heapbedingung: In einem MaxHeap gilt für alle inneren Knoten i: E_i >= E_2i+1 und E_i >= E_2i+2.
Anders ausgedrückt: ein Binärbaum stellt genau dann einen MaxHeap dar, wenn der Schlüssel jedes Knotens mindestens genauso groß ist wie der seiner beiden Söhne.
Beispiel: Folgender Binärbaum ist ein MaxHeap:

Index	0	1	2	3	4	5	6
Element	7	5	6	3	1	2	4

Deutlich zu erkennen ist, dass in dem Array an erster Stelle das größte Element der Folge steht.
Das Finden des Maximums stellt somit nur einen Zugriff auf das Element E₀ dar.

4.2.2.2 MinHeap:
Ein Heap heißt MinHeap bzw. es liegt eine Min-Ordnung vor, wenn für alle inneren Knoten deren Schlüssel kleiner gleich denen der beiden Söhne sind, d.h. es gilt die MinHeap-Bedingung: In einem MinHeap gilt für alle inneren Knoten i: E_i <= E_2i+1 und E_i <= E_2i+2.
Anders ausgedrückt: ein Binärbaum stellt genau dann einen MinHeap dar, wenn der Schlüssel jedes Knotens höchstens so groß ist wie der seiner beiden Söhne.
Beispiel: Folgender Binärbaum ist ein MinHeap:

Index	0	1	2	3	4	5	6
Element	1	2	3	6	4	5	7

Analog zum MaxHeap steht in dem Array an erster Stelle das kleinste Element der Folge.
Das Finden des Minimums stellt somit nur einen Zugriff auf das Element E₀ dar.

Dies sind die beiden Möglichkeiten, wie ein regulärer Heap organisiert werden kann. In der Literatur wird der MaxHeap meist nur als Heap bezeichnet, aus gutem Grund. Denn obwohl man mit beiden Heapordnungen (Min/Max) eine Sortierung durchführen kann, bringt die Verwendung von MaxHeaps Vorteile mit sich, die sie in der Praxis gegenüber MinHeaps hervorheben, wie wir nachfolgend noch sehen werden.

4.2.3 Die Operation Versickern:
Diese grundlegende Heap-Methode wird für den effizienten Aufbau eines Heaps ebenso benötigt wie für die Sortierung an sich. Stellen wir uns vor, wir entfernen das erste Element eines Heaps (also die Wurzel des Binärbaums) und setzen an dessen Stelle ein anderes Element. In diesem Fall hat man im linken sowie rechten Teilbaum der Wurzel je einen Heap, der gesamte binäre Baum stellt im Allgemeinen aber keinen Heap mehr dar, da nicht klar ist, ob die Heapbedingung für die Wurzel und ihre beiden Söhne noch erfüllt ist.
Daher muss das Element in der Wurzel an seine korrekte Position im Baum gebracht werden, sodass dieser wieder einen Heap darstellt, die Heapbedingung also wieder erfüllt ist - hierzu lässt man das Element im Baum "versickern".
Bei der Methode des Versickerns nutzt man die Eigenschaft aus, dass man schon zwei Teilheaps hat und durch Schlüsselvergleiche mit linkem und rechtem Sohn ein einfaches Werkzeug in der Hand hat, mit dem man das Element in den korrekten Teilbaum versickern lassen kann. Dabei geht man wie folgt vor:

Zunächst wird die Gültigkeit des Index des aktuellen Elementes i überprüft. Ist die Forderung 0 <= i <= n-1 nicht erfüllt, endet die Ausführung der Funktion hier.
Es wird getestet, ob das aktuelle Element einen Sohn besitzt, d.h. ob es einen Index gibt, der die Bedingung 2i+1 <= n-1 erfüllt. Hat das Element einen Sohn, so wird dieser zum Vergleichselement und es wird mit Schritt 3 fortgefahren, ansonsten bricht die Funktion ab.
Es wird nun getestet, ob das Element auch noch einen zweiten Sohn besitzt, d.h die Bedingung 2i+2 <= n-1 erfüllt ist. Wenn ja, so wird von beiden Söhnen der größere (MaxHeap) ermittelt und zum neuen Vergleichselement. Ansonsten wird sofort Schritt 4 ausgeführt.
Es wird getestet, ob die Heapordnung verletzt ist. Wenn ja, so wird das aktuelle Element mit dem Vergleichselement getauscht, ansonsten kommt Schritt 5 zur Ausführung.
Das Vergleichselement wird zum aktuellen Element und es wird wieder zu Schritt 1 verwiesen.

Bei der Umsetzung dieses Algorithmus' kann man ein wenig einsparen, was zu folgender Funktion versickern() führt, welche das Element mit dem Index i im Baum versickern lässt:

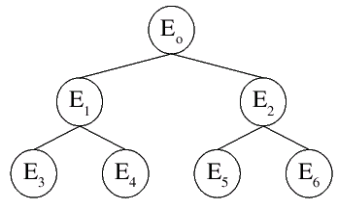
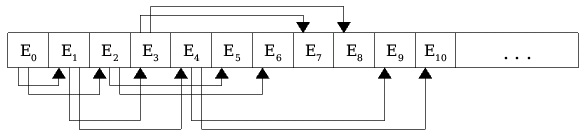
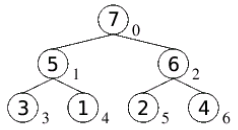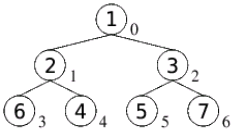void versickern(int a[], int n, int i){		//i=Index des zu versickernden Elementes
  int j, h=a[i];
  if(i<0) return;				//wenn i ungültig, dann abbrechen
  while(i<n/2){					//solange noch Söhne vorhanden sind
    j=i+i+1;					//setze Vergleichselement j auf linken Sohn von i
    if(j+1<n && a[j]<a[j+1]) j++;		//wenn rechter Sohn größer linkem, dann dieser als j setzen
    if(h>=a[j]) break;				//wenn Heap-Ordnung hergestellt, dann abbrechen
    a[i]=a[j]; i=j;				//Element im Heap nach unten versickern
  }
  a[i]=h;					//Element an Endposition einordnen
}

Beim Versickern eines Elementes in einem Binärbaum werden maximal log(n) Vertauschungen durchgeführt, was der Höhe des Baumes entspricht. Daher ergibt sich auch die Zeitkomplexität von O(log(n)) für diese Methode.
Diese Operation reicht bereits aus, um den Sortieralgorithmus und die Konstruktion eines Heaps realisieren zu können, wodurch andere Heap-Methoden im Rahmen dieses Textes nicht weiter betrachtet werden müssen.

4.2.4 Aufbauen eines Heaps:
Bevor man überhaupt zur Sortierung übergehen kann, muss zunächst einmal aus einer gegebenen Folge ein Heap konstruiert werden. Der Erfinder von Heapsort, J.W.J. Williams, hat eine Methode mit einer Komplexität von O(n*log(n)) angegeben. Wir wollen hier hingegen ein Verfahren betrachten, welches von R.W. Floyd entwickelt wurde und einen Heap mit O(n) in linearer Zeit konstruieren kann. Dieses Verfahren stützt sich auf den sukzessiven Aufbau von Teilheaps, von denen je zwei mit deren Vater zu einem Heap verschmolzen werden, indem für den Vater die Operation des Versickerns ausgeführt wird. Die Bedingung für das Versickern, dass die beiden Söhne bereits Heaps sind, ist für Teilheaps mit einem Element trivial erfüllt. Daher können je zwei dieser Elemente mit deren Vater zu einem Heap der Höhe 2 verschmolzen werden, diese zu Heaps der Höhe 3 usw., bis durch das Verschmelzen mit dem Versickern der Wurzel E₀ ein Gesamt-Heap erzeugt wird und die Konstruktion damit abgeschlossen ist.
Bei der programmiertechnischen Realisierung wird dieser Algorithmus wie folgt interpretiert:
Aus einer unsortierten Folge von n Schlüsseln erhält man eine Heapordnung, indem man für die Elemente n/2-1, n/2-2, ..., 0 die Funktion 'versickern()' ausführt.

Neu daran ist der Fakt, dass beim Element n/2-1 begonnen wird. Man muss ein wenig überlegen, um sich vom Funktionieren dieses Vorgehens überzeugen zu können. Dabei kann man leicht erkennen, dass die Blattebene eines vollständigen binären Baumes maximal (n+1)/2 Elemente besitzt. Z.B. hat ein vollständiger Baum mit 31 Elementen 16 Blätter. Will man in diesem Baum nun Heaps der Höhe 2 erstellen, so nimmt man die direkt über den Blättern liegende Knotenebene, deren letztes Element auf der Position n/2-1 liegt (klar: (n+1)/2 Elemente maximal in der Blattebene, also maximal n/2 innere Knoten). Diese Knoten lässt man versickern, geht dann in die höheren Ebenen, die durch einfache Dekrementierung des Arrayindex erreicht werden können und führt dort weiter das Versickern aus, bis die Wurzel erreicht ist. Dass die Wahl von n/2-1 nicht nur für maximal vollständige Binärbäume (wie gerade gezeigt) funktioniert, lässt sich schnell überlegen: entnimmt man zwei Elemente vom Ende des Arrays, so vermindert sich n/2 um nur ein Element - nämlich genau das, dessen Söhne man entnommen hat. Daher ist es korrekt, wenn man dieses Element aus dem Versickern-Prozess ausschließt.

Auf Basis dieser Überlegungen kann man die Methode der Konstruktion eines Heaps nun wie folgt angeben:

void konstruktion(int a[], int n){
  int i;
  for(i=n/2-1; i>=0; i--)
    versickern(a,n,i);
}

Folgendes Beispiel zeigt, wie diese Konstruktion schrittweise erfolgt:

1.) Ausgangssituation: die Schlüssel liegen durcheinander und fernab von jeder Heapordnung im Binärbaum (Array) vor.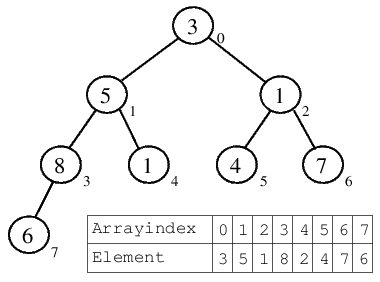
2.) Im Array sind n=8 Elemente vorhanden. n/2=4, also ist n/2-1=3 das Element, von welchem aus nach unten hin das Versickern ausgeführt wird. a[3]=8, mit diesem Element als Wurzel ist die Heap-Bedingung des darunter liegenden Teilbaumes erfüllt (8>=6), sodass nicht versickert werden muss.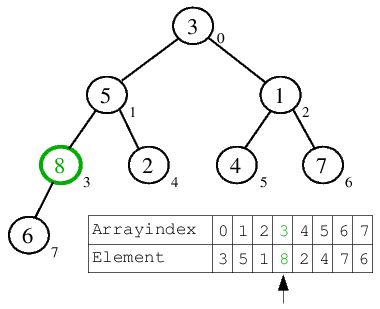
3.) Der Arrayzeiger wird dekrementiert und zeigt nun auf a[2]=1. Hier ist die Heap-Bedingung für den darunter liegenden Teilbaum ganz offensichtlich nicht erfüllt. a[2] hat die zwei Söhne a[5]=4 und a[6]=7. Da a[6]>a[5] ist, wird das aktuelle Element a[2] mit diesem getauscht, "versickert" im Baum. Da anschließend keine Söhne mehr vorhanden sind, bricht der Algorithmus ab und die 1 gilt als versickert.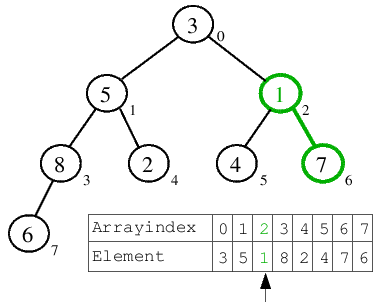
4.) Nach der Dekrementierung des Zeigers wird das Versickern für a[1]=5 ausgeführt, für welches die Heap-Bedingung ebenfalls verletzt ist. Sukzessive wird bei den Söhnen nach dem größeren Element gesucht und mit 5 getauscht. Da 8>2 ist, kommt die 5 zunächst auf deren Platz, um dann noch eine Position weiter über die 6 ans Ende des Arrays zu versickern.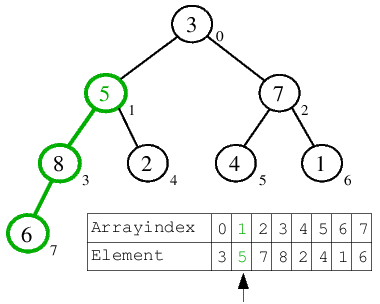
5.) Als letztes Element wird a[0]=3 betrachtet, für welches die Heap-Bedingung natürlich auch verletzt ist. Nach dem Finden der größten Söhne gelangt die 3 über a[1]=8, a[3]=6 und a[7]=5 ans Ende des Arrays.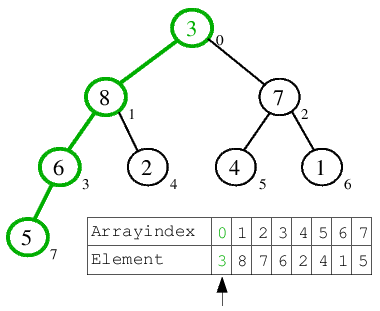
6.) Nachdem das erste Arrayelement versickert ist, gilt der Heap als konstruiert. Schön zu sehen, dass man nun auf das größte Arrayelement über a[0] zugreifen kann und dies nur einen einzigen Schritt erfordert. Die Heap-Bedingung ist für alle Unterbäume erfüllt, sodass es sich bei dem dargestellten Binärbaum auch wirklich um einen Heap handelt.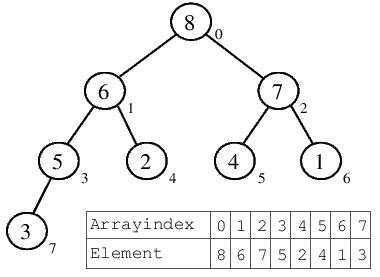

4.3 Der Heapsort-Algorithmus

Mit dem (Max-) Heap als Datenstruktur und der damit verbundenen Operation des Versickerns lässt sich leicht ein effektives Sortierverfahren konstruieren. Die Vorgehensweise dabei ist so logisch wie einfach: entferne zunächst das größte Element auf Position 0, setze dafür das letzte Arrayelement und lass dieses versickern - wiederhole diesen Vorgang bis kein Element mehr im Array vorhanden ist.
Direkt damit verbunden ist auch der Vorteil der Verwendung von MaxHeaps: anstatt für die Speicherung der sortierten Folge ein zusätzliches Array mit n Elementen zu verwenden, können das Element auf der Position 0 und das letzte noch zu betrachtende Heap-Element vertauscht werden, wodurch das momentan größte Element auf seinen endgültigen Platz im sortierten Array gelangt. Die sortierte Folge wird also von hinten nach vorn durch sukzessive Entnahme des ersten (größten) Elementes aufgebaut, wodurch das Gesamt-Array zwar seine Heap-Eigenschaft verliert, dies uns bei der Zielstellung der Sortierung einer Folge aber nicht stören soll.

Folgendes Beispiel soll die Arbeitsweise von Heapsort illustrieren. Verwendet wurde dabei der in 4.2.4 erzeugte MaxHeap, sodass wir uns den Schritt der Konstruktion eines Heaps sparen können.

1.) Ausgangssituation: der oben konstruierte MaxHeap.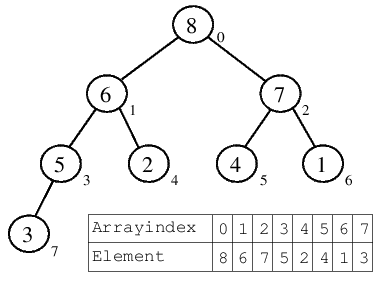
2.1) 8 wird an das Ende des Arrays eingefügt, das dortige Element 3 wird dafür als neue Wurzel gesetzt, was ein Versickern entlang des grünen Pfades zur Folge hat.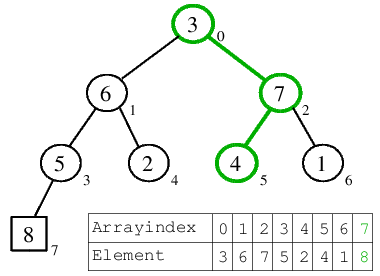
2.2) Nach dem Versickern der 3 steht die 7 als größtes Element auf der Wurzel-Position.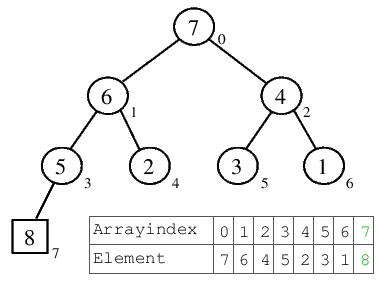
3.1) 7 wird vor die bereits fest gelegte Position der 8 eingefügt, mit der dortigen 1 getauscht, welche anschließend versickert.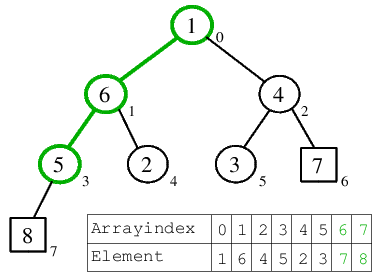
3.2) Nach dem Versickern der 1 steht die 6 auf der Wurzel.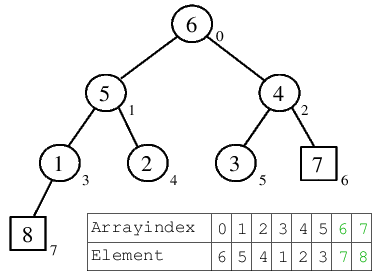
4.1) 6 wird ans Ende des Rest-Heaps verschoben, die 3 von dort kommt in die Wurzel und versickert eine Position nach links, bis der Rest-Binärbaum wieder einen Heap darstellt.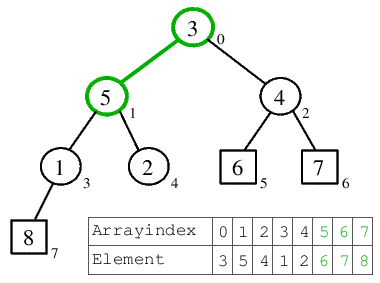
4.2) Nach dem Versickern der 3 steht das nächstgrößte Element, die 5, in der Wurzel.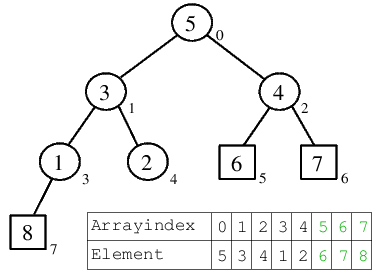
5.1) 5 wird mit der 2 ans Heap-Ende getauscht, erhält dadurch seinen festen Platz in der sortierten Folge. Die 2 muss nun versickern und bewegt sich dabei eine Position nach rechts, wo das Ende des Rest-Heaps erreicht ist.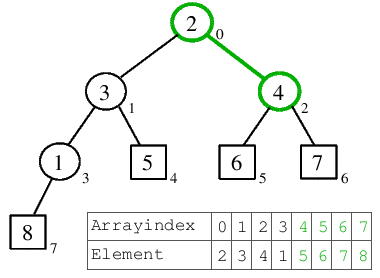
5.2) Nachdem die 2 versickert ist, steht mit 4 das nächst kleinere Element in der Wurzel.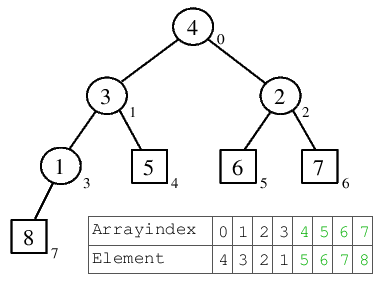
6.1) 4 kommt ans Heap-Ende, wodurch die 1 in die Wurzel gelangt und eine Position nach links versickert, bevor die Ordnung des Rest-Heaps wieder hergestellt ist.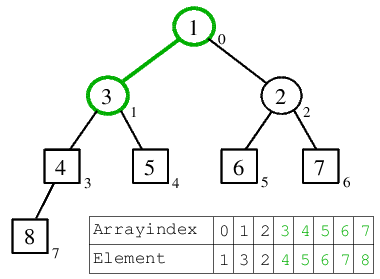
6.2) Nach dem Versickern der 1 steht mit der 3 das nächst größere Element zum Einordnen bereit.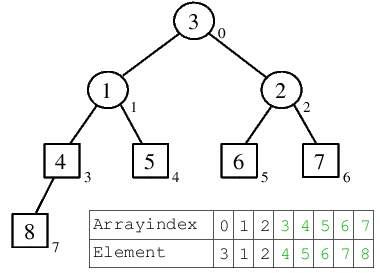
7.) Die 3 wird eingeordnet, die 2, welche dadurch in die Wurzel kommt, verletzt die Heap-Ordnung nicht, wodurch nicht versickert werden muss.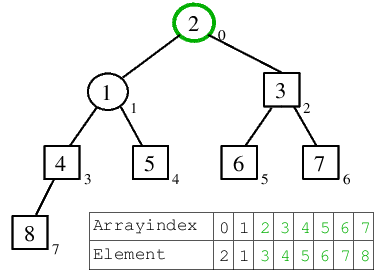
8.) Die 2 kommt ans Ende des aus nur noch 2 Elementen bestehenden Rest-Heaps. Die 1 kommt in die Wurzel. Da der Heap aus nur noch einem Element (der Wurzel) besteht, erfolgt kein Versickern dieser.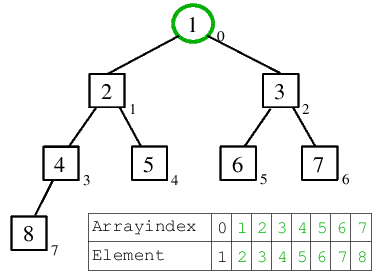
9.) Die finale Darstellung: alle Elemente wurden sortiert von hinten nach vorn im Array eingefügt, was nun in aufsteigender Reihenfolge vorliegt. Klar, dass dies keinen Heap mehr darstellt - das soll uns aber nicht weiter stören.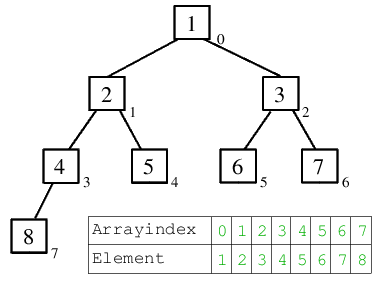

4.4 Zur programmiertechnischen Realisierung

Der C-Code für Heapsort an sich ist nicht schwer: zunächst wird aus der beliebigen Folge ein Heap aufgebaut, was bei der sofortigen Wahl des Heaps als Datenstruktur allerdings entfällt. Dann folgt die Soriterung: man tauscht n-mal das erste Element mit dem gerade letzten und stellt dann die Heap-Ordnung wieder her, indem die Funktion versickern(a,i,0) ausgeführt wird, wie es folgender Code zeigt:

void heapsort(int a[], int n){
  int i, tmp;
  konstruktion(a,n);
  for(i=n-1; i>=0; i--){
    tmp=a[0]; a[0]=a[i]; a[i]=tmp;
    versickern(a,i,0);
  }
}

4.5 Laufzeitbetrachtungen

Die Zeitkomplexität für den Aufbau des Heaps beträgt wie schon beschrieben O(n). versickern() wird in O(log(n)) ausgeführt - ganze n-mal. Dies führt zu einer Gesamtlaufzeit von O(n)+n*O(log(n)), was nach den allgemeinen Rechenregeln der O-Notation zu max{O(n),O(n*log(n))} und somit zu O(n*log(n)) vereinfacht werden kann.
Heapsort ist nicht sonderlich schnell, in praxi benötigt o.a. Implementation ein Vielfaches der Zeit von Quicksort und ist in etwa vergleichbar mit dem grundlegenden Straight-Radix-Sort-Algorithmus. Seine Relevanz behält es trotzdem, zumal es wie Mergesort eine worst-case-Zeitkomplexität von O(n*log(n)) besitzt und wie etwa Quicksort keinen zusätzlichen Speicher benötigt.

[ Zurück zum Inhaltsverzeichnis ]